20241105_活動報告

Contents

1 はじめに
2 活動報告
3 おわりに

はじめに

　どうも。皇帝の宝石・アレキサンドライトです。更新が遅れてしまいましたが、活動報告をしていきたいと思います。

活動報告

　いつも通り多種多様なボードゲームやカードゲームが嗜まれていました。

　また、自主ゼミも行われました。本日は3名の方が発表して下さいました。皆さん素晴らしい発表だったと思います。（私も発表したのですが、少し長くなってしまった気がします…。反省）

おわりに

　マイコン研は毎週火曜・金曜の6時からサークル会館にて活動しています。是非遊びに来てみてください。

自主ゼミの補足

　自主ゼミで説明できなかった部分の補足をしようと思います。

　まず、私の発表テーマは「早く決着が着くじゃんけん」を求めることです。そして、その結論ともいえるのが「RPSDM (Rock-Paper-Scissors for Diversity and Minorities)」と私が命名したじゃんけんなのですが、そのルールが以下です。

各プレイヤーはあらかじめ決められた手の中から好きな手を出す
各手のうち最も少ない手を出した人が勝ち
最も少ない手が2つあった場合はその2つの手で多様性じゃんけんの勝敗表に基づき勝敗を決める
最も少ない手が3つ以上あった場合はあるルールに従い勝者を決める

　「多様性じゃんけんの勝敗表」はゼミでも説明しましたが、使用する手を円周上に等間隔に並べた時に、自分の手から見て相手の手が反時計回りに180°以上離れていれば相手の勝ち、そうでなければ自分の勝ちとするものです。

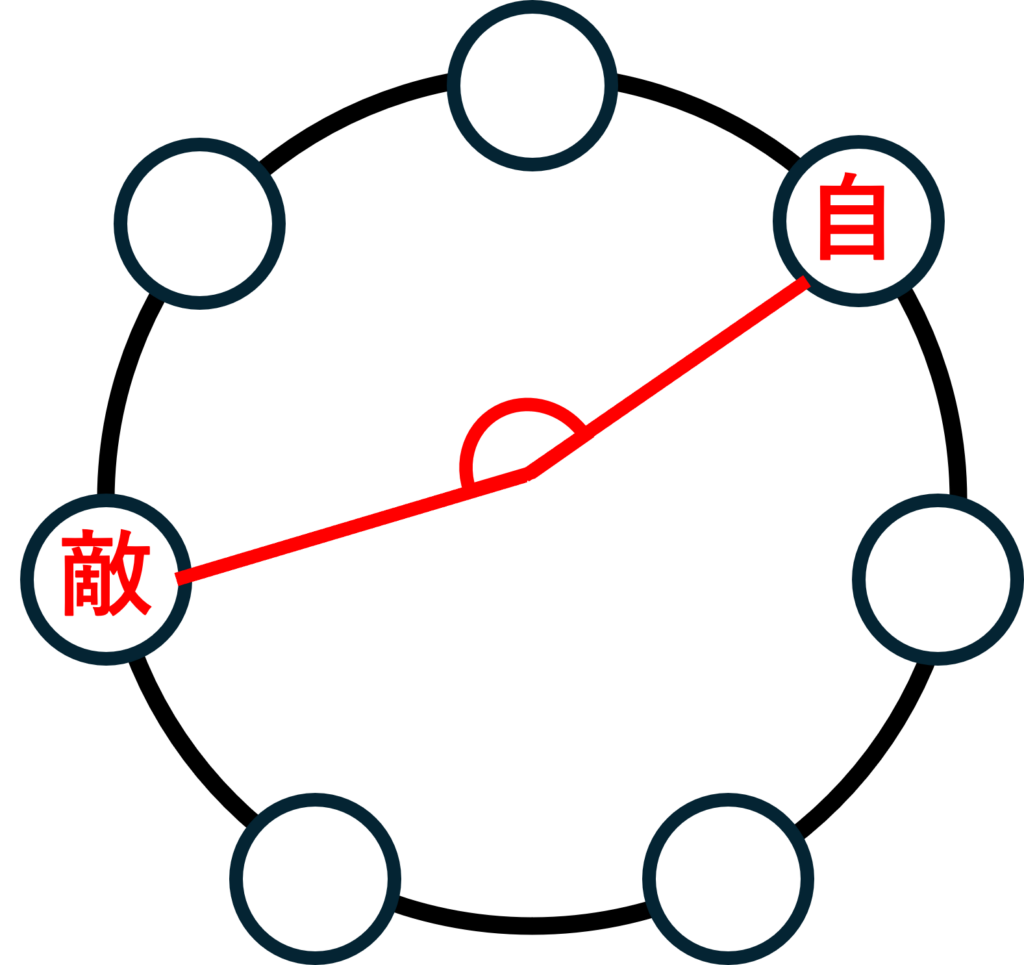
　例えば、上の例の場合は自分の勝ちになります。

　そして、最も少ない手が3つ以上あった場合のルールをゼミで説明できなかったので、それを補足したいと思います。

　まず、最初に断っておきますが、これから紹介するルールはあくまで一例であり、3つ以上異なる手が出されたときに勝者が一意に定まりさえすれば何でもいいです。ただ、なるべく単純で直感的なルールの方が望ましいので、その一例を紹介します。

ルール①

最も少ない手のうち隣接しているものを1つの塊とみなし、「島」と呼ぶ。また、島に含まれる手の個数を島の「大きさ」と呼ぶ。
最も大きい島の数が1つのとき、その島に含まれる手のうち（円の中心から見て）最も右にあるものを勝者とする。

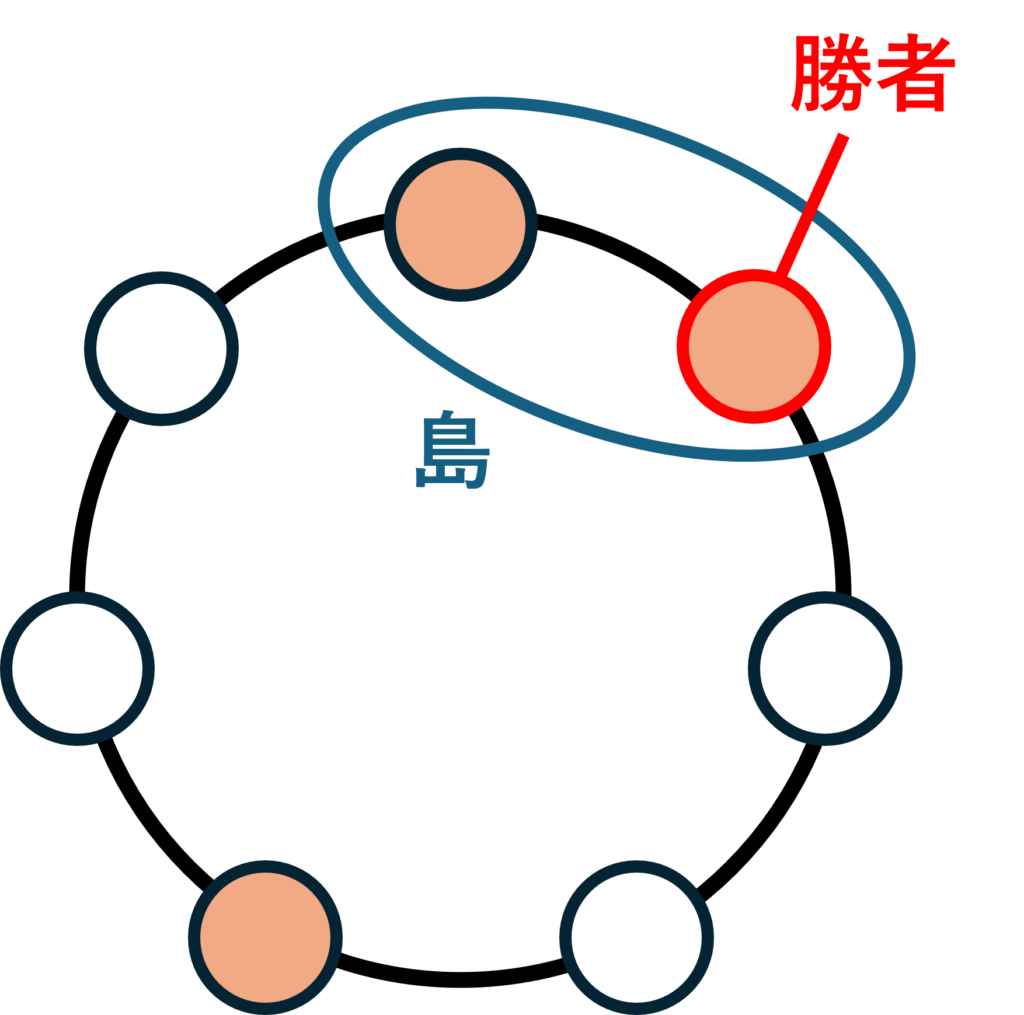
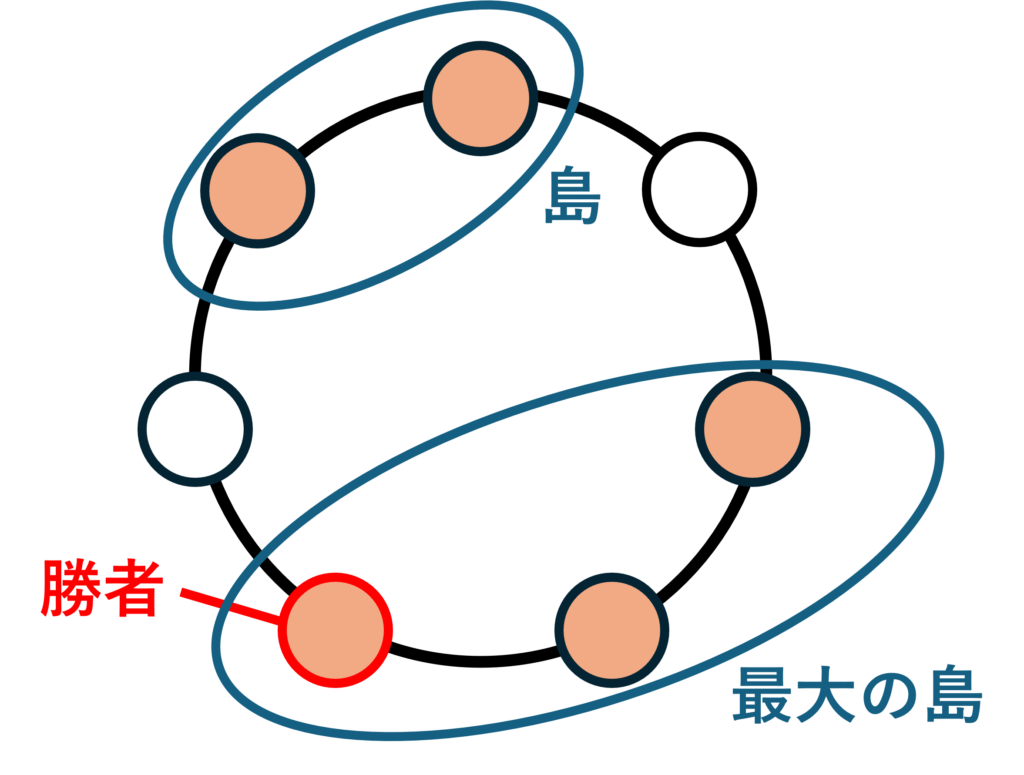
　RPSDMは基本少数派が勝つルールですが、この場合はより大きな集団に属しているものを勝者とします。（その方が勝者を決定しやすいので…）。なお、「円の中心から見て右」というのは、円を地面におき、その中心に立って島を見た時に右にある方ということです。「時計回りに正の方向」と言ってもいいでしょう。左でなく右が勝つ理由は、島に属する手同士で多様性じゃんけんを総当たりで行ったときに、一番右にある手が最も勝数が多くなるからです。

ルール②

最大の島が2つのとき、それぞれの島に含まれる手のうち（円の中心から見て）最も右にあるものを「代表者」といい、代表者同士で多様性じゃんけんの勝敗判定を行い、勝者をこのじゃんけんの勝者とする。

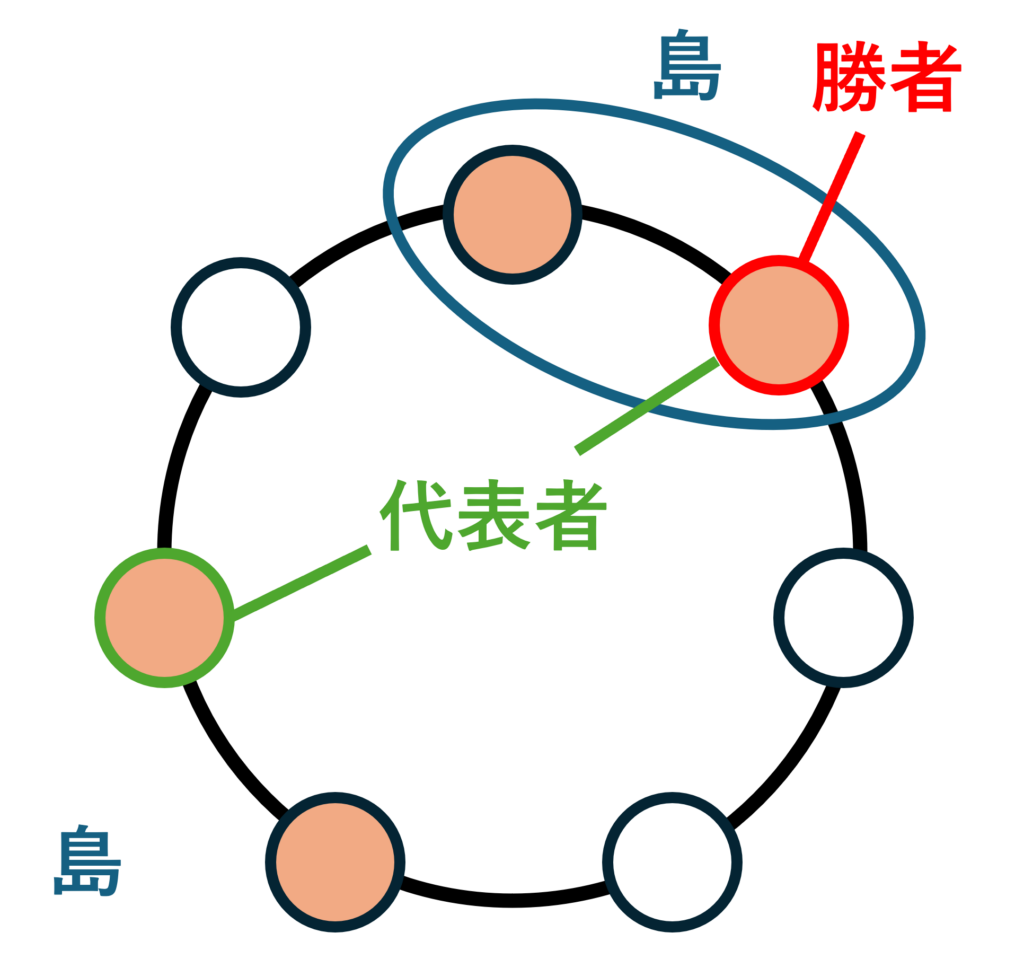
　これは比較的わかりやすいルールかと思います。「代表者」は最大の島が一つだけの場合の勝者であり、その勝者同士が多様性じゃんけんで決着をつけるわけです。

ルール③

最大でない島及び出されていない手は全て同様に扱い、「海」と呼ぶ。
最大の島が3つ以上のとき、海を1つだけ挟む島同士を1つの島のように扱い、これを「1次擬島」と呼ぶ。
最大の1次擬島が2つ以下の場合、最大の島が2つ以下の場合と同様に勝者を決める。
最大の1次擬島が3つ以上の場合、海を2つ挟む島同士を「2次擬島」として扱い、同様に考えて勝者を決める（2次擬島を構成する際、最大でない1次擬島がある場合は、それらは海として扱う）。
このような工程を勝者が決まるまで行う。

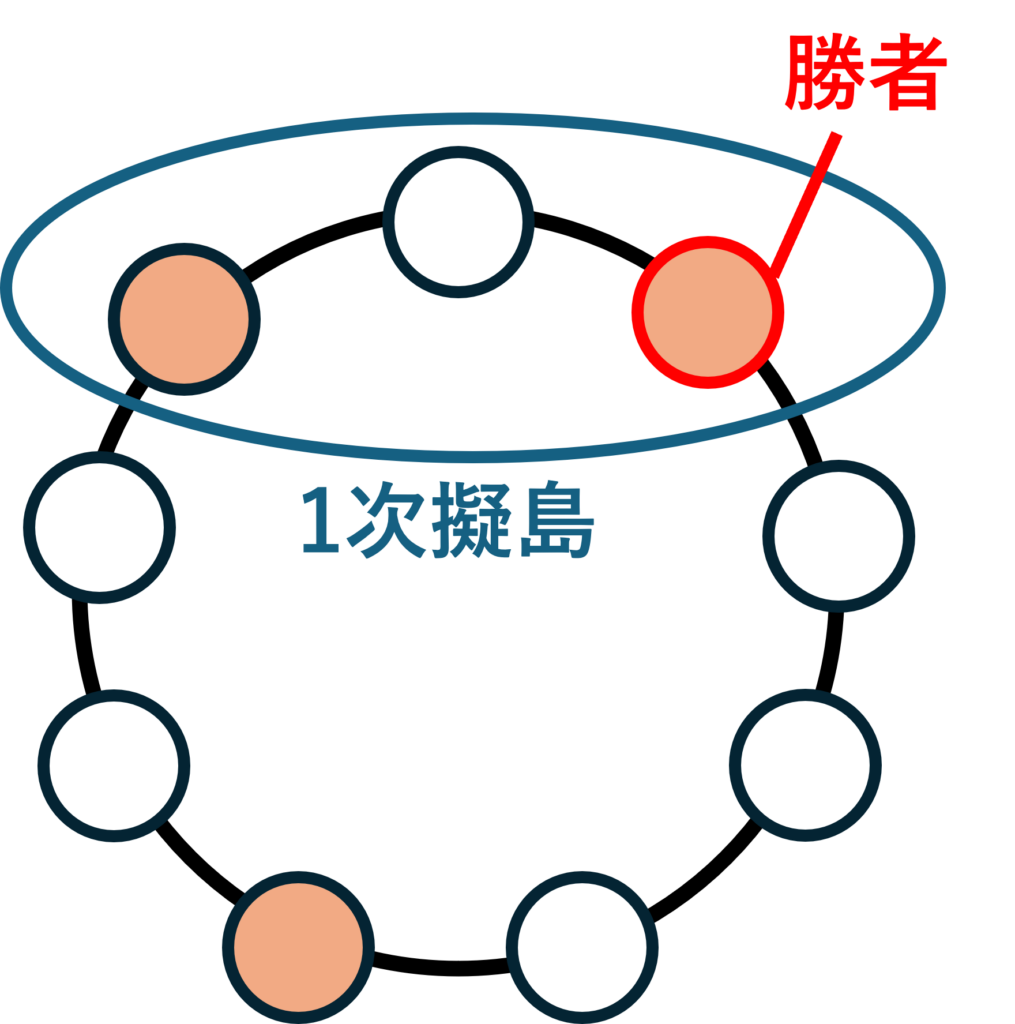
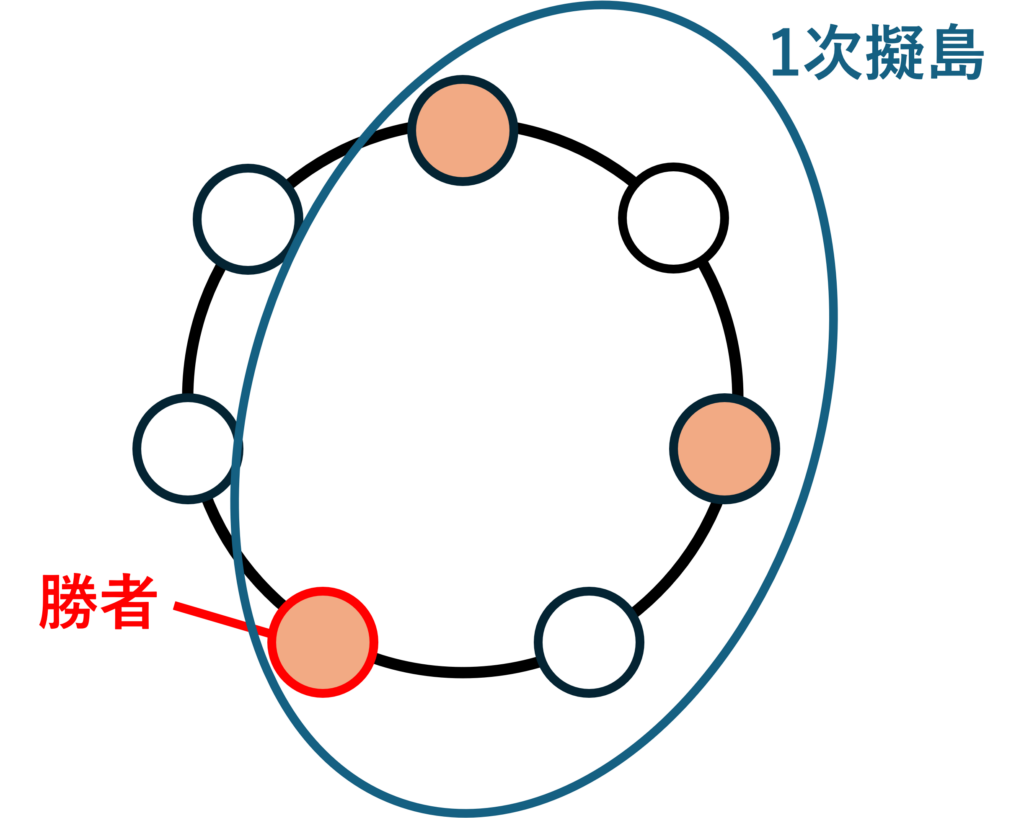
　3つ目のルールは少し分かりづらいですが、最大の島が3つ以上ある場合はそのまま勝者を決めるのは少し難しいので、間の海を含めて擬似的な島を作ってしまおうという考え方です（ちなみに「擬島」は「ぎとう」と読む造語です。ただの「島」と区別したかったので便宜的に名付けました）。これを繰り返すことによっていつかは最大の島が2つ以下になり、勝者を決定することができます。なお、2次以上の擬島が必要になるのは手の数が11以上の場合なので、ゼミで紹介したRPSDM-3、RPSDM-5、RPSDM-7の場合は1次擬島までを考えることで決着をつけることができます。

例外

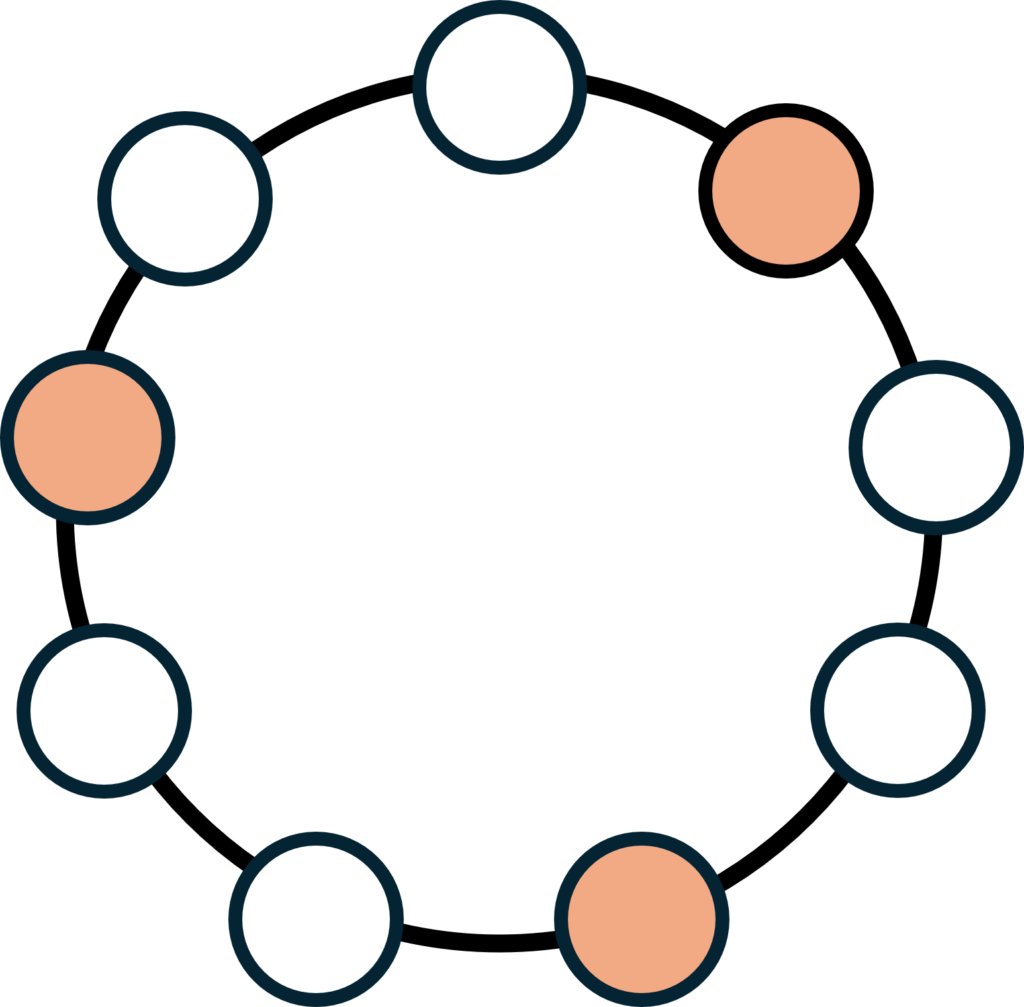
　上記のルールで基本的には勝者を一意に決定することができますが、例外もあります。それは上図のように手が円に対して対称に分布した場合です。この場合、ルール通りに勝者を決定しようとすると、1次擬島は作れないので2次擬島を作ろうとしますが、そうすると全体が一つの擬島になってしまい、勝者が決定できなくなります。無理矢理に新しいルールを作って勝者を決めようとすることもできますが、「各手の強さは等しい」という前提を崩さずにそのようなルールを作ることは不可能です。そのため、このような場合にはあいこにするか、最も少ない手（上図の手）を出した人全員を勝者とする、あるいは最少から2番目の手を出した人の中で勝者を決めるなど、別のルールを設ける必要があります。ですが、実は手の種類を素数にすることによって対称性を無くし、このようなことを回避することができます。ですので、ゼミで紹介したRPSDM-3、RPSDM-5、RPSDM-7ではこのようなことは起きません。