はじめに
お久しぶりです。shelfです。皆さんいかがお過ごしでしょうか。私は完全週休四日せいでのんびりとしたキャンパスライフを送っています。そのせいで火曜日が全休になり、行かないことが増えてしまったのですが、自己紹介ゼミがあるとなるとこれはいかなければならないなと思いました。そのためこれからは頑張って火曜日も行くかなと思います。まぁ気分ですけど。ところでページの最後の方に新しい拡張の購入なしでできる正式ルールのドミニオンの拡張の例を載せておきますので、だれかやりましょう!
活動報告
ゲーム編
Monopoly
さあ、今日もやってきました。モノポリーのコーナー!モノポリーはおもしろいなぁ、そうに決まっている。

この日は四人で始めたはずなのですが、ある人が確か、
\[10(ぞろ目)\to 9\to 11(Go to Jail)\to 脱出\to 忘れた\times 2\rightarrow Go to Jail \to \cdots \to \circ亡\]
(上のLaTeXについてはpolyfill.ioっていうやつを使用していたのですが、どうやらよくないらしいので原文のまま表記しました(2/7更新))
っていう悲惨な経路をたどった気がするのはおいといて、みんなすごくモノポリーが好きみたいですね。そしてこのゲーム毎回ボードウォークが大事になっている気がします。楽しいからいんですけど。にしても初手から速攻でJailに二回も突っ込まれた人はどんな悪行をなしたのですかねぇ。というかこのゲーム、途中からJailにいるほうがシャバにいるよりかいいって、なんかどろどろとした世界ですよね。僕は、リスキーでも動いてる方が楽しいと思います。
その他
この日は総会の影響もあってか人がだいぶいてわちゃわちゃ楽しくやってましたね。






いつも通りのIt’s a wonderful worldや、デュエマ、美術対戦などがやられてたみたいですね。あのトポロジーをテーマとしているやつも面白くていいですよね!
Carcassonne(カルカソンヌ)

皆さんあれのもともと入ってる拡張やったことありますか?観光地、川、修道院長っていう拡張が入っているんですけど、この日は、川ともう一つ特殊ルールでやってました。川というのは泉のタイルから下方向に対して川を伸ばすことができます(それだけ)。まぁ、左の写真からわかる通り、その川沿い\((\neq 北海道札幌市南区川沿)\)に街や修道院があったりします(ところで修道院と教会って違うらしいですけど、一般人的にごっちゃになっちゃったりしますよね)。もう一つのルールというのは、得点が二倍になるコマを用意するってことです。そいつが得る得点はすべてに倍になります(ゲーム終了時に未完成の街の上にいるときのみ得点は入らない)。この試合はかなり白熱しました!
ところで、皆さん、カルカソンヌって意外と拡張多いみたいですね。
あと、こんなのも見つけました。
ところで、この”カルカソンヌ”っていうのはどうやら、フランスの地名らしいですね。
総会編
とても活発に議論が行われていて(僕がダルがらみをしてのばしたような気が少しして申し訳ないのですが)とてもよかったと思います。どうにかしてwi-fiが使えるようになってほしいですよねぇ。自己紹介ゼミの話も上がっていて、自己紹介ゼミはみんな好きなことを語れるので総じて楽しいものになると相場が決まっているので行きたいものですよね。初めての方も、自分の趣味を全開にして下さいね!真面目なトピックとして飲酒ゼミとか献血のゼミとかもあってこの日はいろいろ学びの多い日でもあったのではないのでしょうか。ちなみに、僕はとある理由であと9か月しないとお酒を飲めないので(泣く)。あとは献血の話とかもあったのですが、予想以上に多くの人がしててびっくりです。
最後に
皆さん、別のことがしたくても人の話はしっかり聞きましょう。
ドミニオンには、サプライに並んでいろいろな山があったりすることがあり、新たなカードを必要としない拡張を教えます。
①イベント(冒険、帝国、移動動物園、略奪、プロモ):カードを購入するのと同じような感覚で王国(サプライ)にあり、購入権と必要な金を使って購入できる。それを購入すると、それに書かれている効果を実行する。ex)焚火(冒険):あなたの場の銅貨2枚以下を廃棄する
②ランドマーク(帝国):特定の条件を満たしたとき、勝利点を獲得する。ex)浴場:あなたが何もカードを獲得せず自分のターンを終えるとき、この上から2勝利点を獲得する。/準備:プレーヤー一人につき6勝利点をこの上に置く。
③プロジェクト(ルネサンス):ゲームで一度購入するとゲーム終了までその効果が強制で続く(任意効果のものも存在)、同一のプロジェクトは再購入不可、廃棄不可。ex)大聖堂:あなたのターン開始時に、手札を1枚廃棄する。
④習性(移動動物園):アクションカードを実行するときそのカードの効果の代わりに、この習性の効果を利用してもよい(持続では最初に選択する、玉座などで2回使用されるカードは都度選べる)ex)フクロウの習性:手札が6枚になるようにカードを引く
⑤特性(略奪):ランダムなサプライの山一つに特殊な効果を付与する。ex)安価な:安価なカードのコストは1金下がる。
⑥へそくり(プロモ、カード):裏面が特殊なカード、効果:5金で購入できる財宝カード、2金、これを含めて山札をシャッフルするとき、これを山札の好きな場所に加えてもよい(山札の中を見てはいけない)。
(⑦”同盟”(同盟):サプライに”好意”を与える同盟の拡張のカードがあるとき(?)、同盟の拡張のカードが与える”好意トークン”を使用することで、”同盟”というサプライに置いてあるカードを使用することが出来る(“同盟”が場にあるとき、各プレーヤーは1好意を得る、そのため1回のみ使用が可能であるがそれだけのためにそれを無理やり入れるというのは微妙なので):ex)平和的教団:あなたの購入フェイズの開始時、好意を好きなだけ支払い、その枚数の手札を廃棄してもよい。)
続きを読む
なんか今日、メインの方もそうですが謎の領域もあまりにも書きすぎてしまいました。一応、ウェブページだけでも楽しくなれるように書いていますので、参加した人もしてない人もページを楽しんでください。あと、前回の謎解きはこのページのどこかにまたあるので探してみてください。
ヒント
続きを読むを押した後、謎の領域の下の方をうまいこと五回くらい押すと?
あのー、ほかのコーナーを大量に書いてしまったので、ここも大量に書くのはびみょいと思い手短に番外編ということでこの紹介をします。次に書くときはある晴れた日のことでも書く予定です。
皆さん、実はAbema独占配信で〈物語〉シリーズの新シーズンが7月6日から始まるのを知っていましたか?確か現在もAbemaで無料で週末に化物語から順々に公開されていたきがします。ところでこれから始まるシリーズに向けて、過去作の振り返り動画だったりキャラ紹介動画だったりがYoutubeおよびAbemaにあがっています。興味のある人はぜひ。新シリーズでの楽曲はYOASOBIのUNDEADのようです。どうやら楽曲をめぐってはファンの間で賛否両論もあったみたいですねぇ。まぁ、今回は手短ということで、この程度にしておきましょう。
謎の領域\(D\)は半径\(r\)の無限次元球であり、その体積は\[D=\lim_{n\to \infty}V_n(r)=\lim_{n\to \infty}\int\cdots\iint_{\{x_1^2+x_2^2+\cdots+x_n^2\leq r^2\} }dx_1\cdots dx_n\]である。\(r=1\)のとき\(D\)即ち\(V_n(1)\)を求めよ。また\(V_n(r)\)はガンマ関数と指数関数などを用いて表すことができる。その\(V_n(r)\)表せ。また\(V_n(r)\)を、\(r=1,x=n\)として\(x,y\)平面上にグラフを連続的にかいて、\(\lim\limits_{x\to 0}V_x(1)\)の値を求めよ。
答え
\[V_n(1)=0,V_n(r)=\frac{\pi ^\frac{n}{2}}{\frac{n}{2}\Gamma (\frac{n}{2})}r^n,下図,\lim\limits_{x\to 0}V_x(1)=1\]
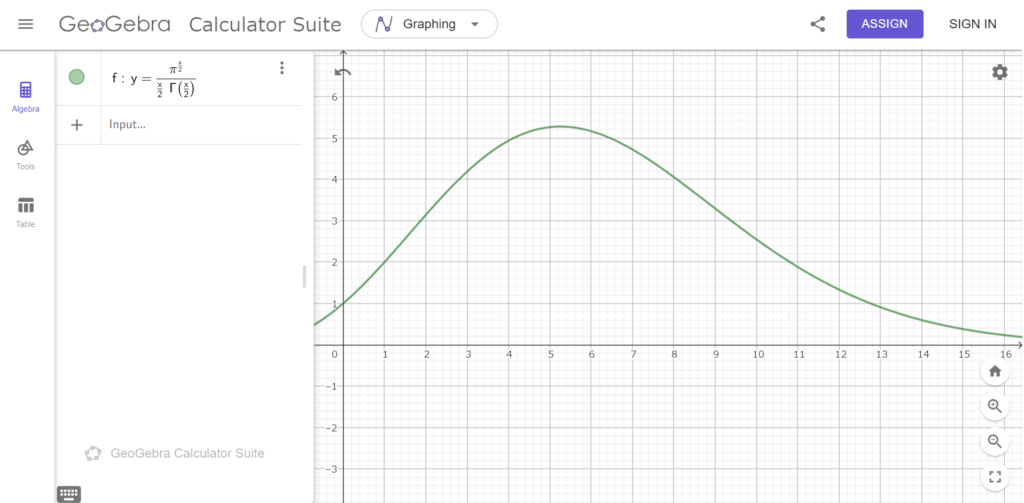
これ実は、\(r\)の値によって収束値が結構変動するんですよね。
geogebraを使用、https://www.geogebra.org/calculator
お疲れ様です。では、前回の隠し場所をお教えしましょう。
ヒント①:メタディスクリプション(活動報告のページからこのページを探すときにPC版だと表示されます。スマホ版だと画面を横にすると表示されるようです。)に73
ヒント②:画像の名前(画像の名前の頭文字(って言っておけばよかったですね)を読んでいくと2nd\(\cdots\)のあとに、unnamedなんちゃらってファイルがあって、それを”[“と、”]”と読み解けば答えとして11が出てきます。)
ヒント③:現在表示されている場所と同じ場所(今回はsafariに対応するようにコードを組み替えました)、答えは1
ヒント④:F12を押した後に表示されるコンソールに書かれています。答えは18
ヒント⑤:ヒント④に表示されたアドレスを押し、コメントアウトされた文章中にURLが載っています。そのURLを入力するとあるYoutubeにたどり着きます。そこからなんやかんやで答えが92とわかる。
これらの答えは原子番号に対応しており、それに対応する元素記号を順に並べるとTa Na H Ar Uとなり、こたえはTANAHARUです。簡単だったかな?
なんとも、毎回こんなに手を込んでいるとすぐにネタ切れを起こしそうで困ったものではあるのですが書きたいものは書きたいのです!
ここまで読んでくれてありがとうございます。それではまた次回。
はずれ
ここには何もないけど、、、
あたり
お疲れさまでした、ちなみにはずれも見つけた?
なんだこの自己満ページw(ここまでたどり着いた人がいれば教えてください!)